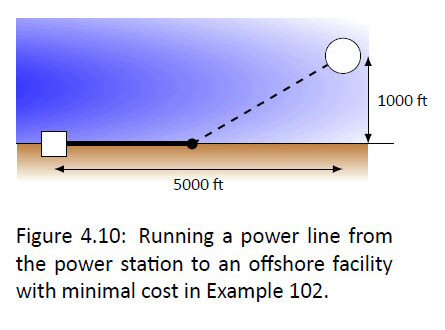
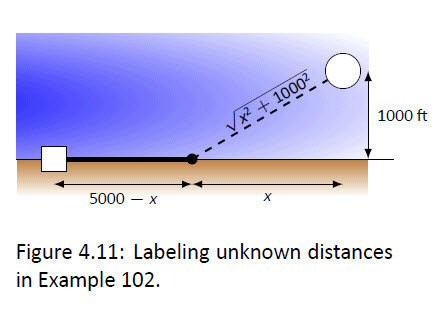
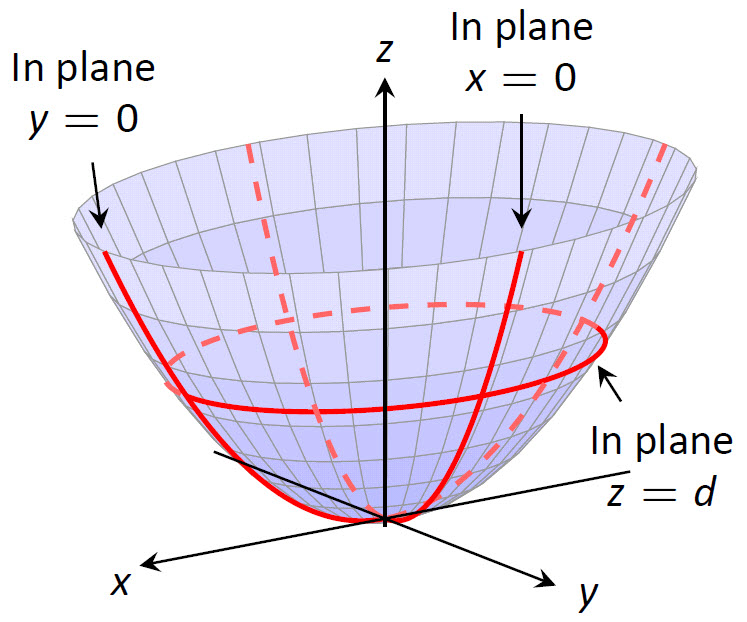
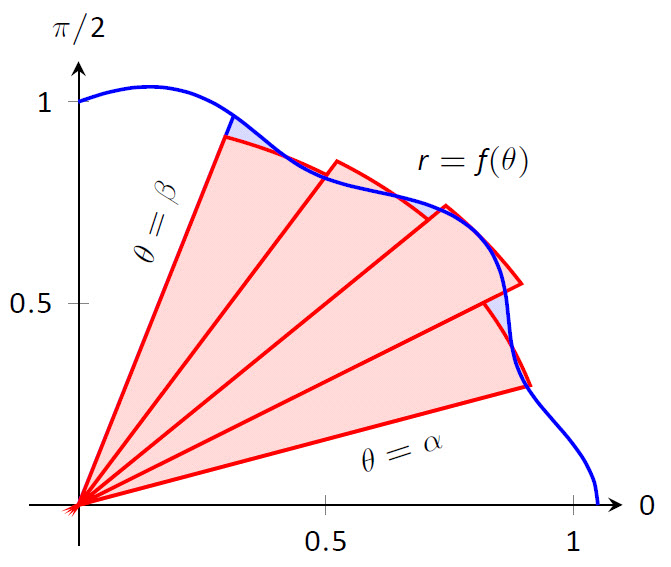
Features
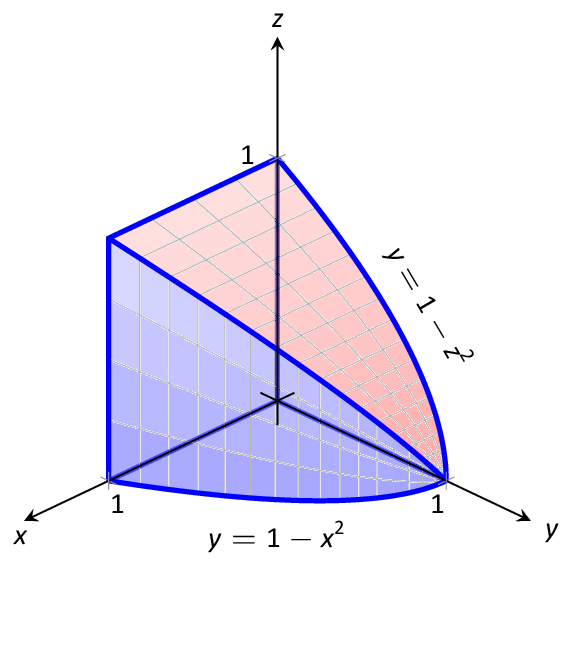
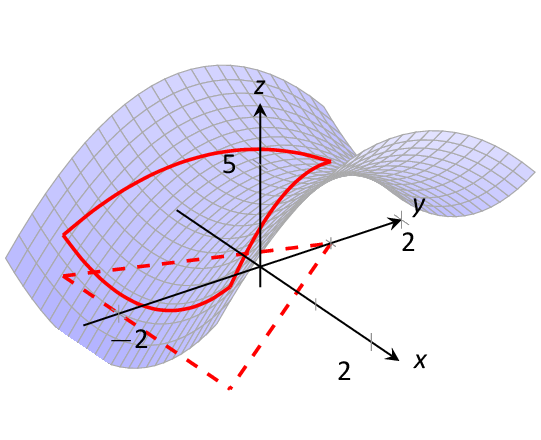
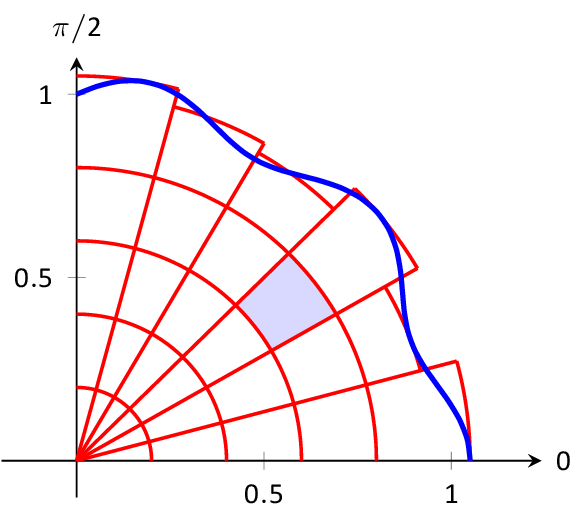
Interactive, 3D Graphics: Introduced in Version 3.0, nearly all images of objects in space, whether curves, surfaces or solids can be manipulated allowing the student to better understand the illustration. The video below gives a short demonstration of some of what the reader is capable of doing.
A few notes about these graphics:
This feature is only available on desktop versions of Adobe Reader/Acrobat. To my knowledge, no other .pdf viewers support the interactivity. Other views should open the .pdf just fine; the reader just won't be able to manipulate the graphics.
To activate the image, click on it. To rotate, click/drag. To pan left/right, up/down, use CTRL+click. When the mouse is over the image, a scroll wheel allows zooming in/out. Right click on the image for more options, including changing the lighting & the perspective.
An effective way to look closely at an image is to first zoom in on the .pdf file itself, making the graphic large on the screen. Then zoom in on the graphic.
The 3D graphics add significantly to the file sizes of the .pdf's. On the Download page, one can get a color .pdf of the text without the interactivity. The images all look the same, they just cannot be manipulated.
Explanatory Text: Some texts seem to follow a "Definition - Theorem - Example" flow, where one learns to do something without really understanding what it is they are doing nor why they should be interested. APEX Calculus strives to explain new ideas, motivated by previous material or everyday life.
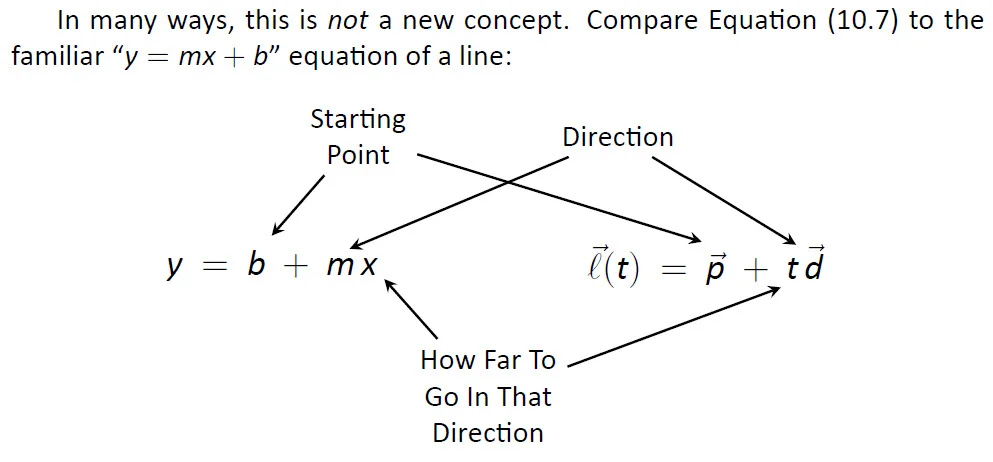
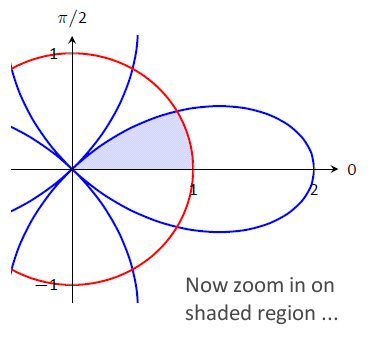
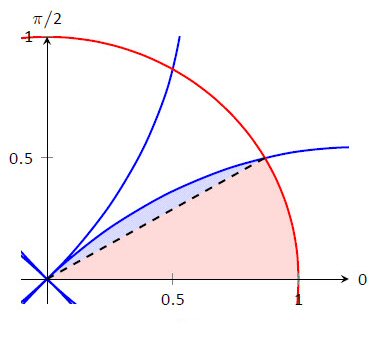
One example of the unique explanations contained in APEX Calculus is shown here. Students often struggle with vector-valued functions, even with "simple" functions whose graph is a line. The illustration shows how the old concept of "a line is defined by a point and a slope" is essentially the same as the new concept of "a line is defined by a point and a direction."
Examples: Every text contains lots of examples, and APEX Calculus is no different. Version 4.0 contains nearly 500 examples that seek to demonstrate the what, how and why of calculus.
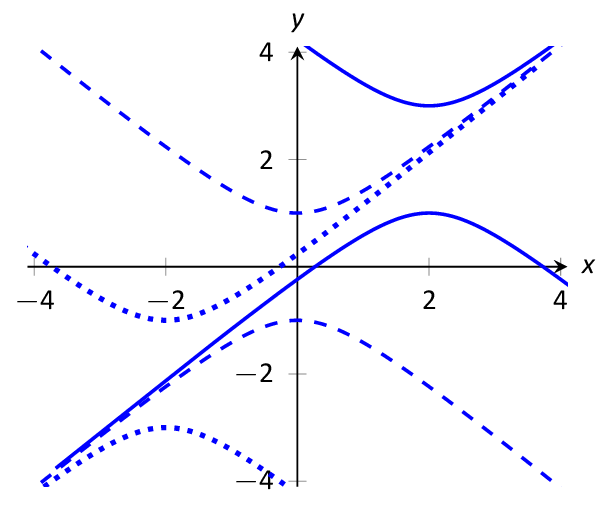
Graphics: Textbooks printed by traditional publishers contain great graphics produced by professional graphic designers. Some open texts have not-so-great graphics. The graphics of APEX Calculus were produced to do more than meet a need - they were produced to impress. Using the power of LaTeX & pgfplots, all 2D images are vector-based meaning they look great no matter how far you zoom in, and the 3D images, made with Asymptote, are interactive.
Space for notes: Each page of text has 2" of white space at the bottom for notes. Students can write their thoughts at the bottom of the page as they read, or put their class notes there as they following similar examples in class. Students writing in their books is a great thing; it reinforces the fact that this is their book, helping break them from the mindset of "I'll just sell this back when I'm done."
Exercise Sets: We all know students need to practice. While a generalization, the following seems to be true: traditional texts have "too many" exercises, and many open texts contain "too few." I hope you'll find that the number of exercises found in APEX Calculus is "just right."
How can a text have "too many" exercises? When a exercise set contains 100+ problems, it can be challenging for instructors to choose which to assign. Students are easily daunted by the selection when studying on their own: should they practice them all? Are some more important than others?
Some sections do need lots of exercises. When learning the Chain Rule, students need lots of practice, so it makes sense to have a lot of problems to choose from. But other sections ... not so much.
Few Proofs: APEX Calculus contains only a few proofs of the 125+ theorems in the text. Why is this a good thing?
Most calculus students - high school seniors and college freshmen - do not know how to read a traditional mathematics textbook, much less a mathematics research paper. I generally read math papers in at least two passes: the first gives me a general idea of what the paper is about (wherein I skip the proofs) and in the second pass, I dive in to understand the proofs. My calculus students, when they finally dig up the nerve to actually read the book - and not just look for an example that matches the homework exercise - quickly get bogged down in details that they frankly don't need to know right now. I believe there is great pedagogical value in giving students confidence that they can read and understand a math book; in upper level courses, we can teach them the concepts of a proof. So APEX Calculus skips most proofs, and focuses on explaining what a theorem says, how to apply it, and why it matters.
Having said all that, a future project is to write a supplemental text that contains only the theorems and their proofs.
Hyperlinks: The PDF version of the text was produced with LaTeX's hyperref package, so when an exercise says "Use Theorem 8.3.1 to evaluate ...", students can click on "Theorem 8.3.1" and be taken to the page containing ... (you guessed it) Theorem 8.3.1.